Circunferencias Congruentes

Dos figuras son congruentes si coinciden cuando colocamos una sobre la otra, dos circunferencias son congruentes si tienen el mismo radio. Por ejemplo, las figuras siguientes.

Triángulos congruentes según el criterio LL (lado-lado-ángulo)

Se dice que el triángulo ABC es congruente con otro DEF si sus lados respectivos son congruentes y sus ángulos respectivos también los son.

Dos triángulos son congruentes si tienen dos lados congruentes y el ángulo opuesto al lado de mayor medida, también congruente.

 

Triángulos congruentes según el criterio LLL (lado-lado-lado)

Se dice que el triángulo ABC es congruente con otro DEF si sus lados respectivos son congruentes y sus ángulos respectivos también los son.

Dos triángulos son congruentes si tiene sus tres lados respectivamente congruentes.

 

Triángulos congruentes según el criterio ALA (ángulo-lado-ángulo)

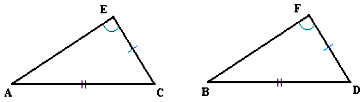
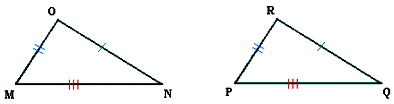
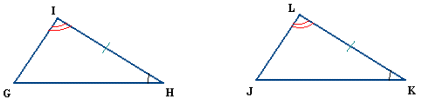
Se dice que el triángulo ABC es congruente con otro DEF si sus lados respectivos son congruentes y sus ángulos respectivos también los son.

Dos triángulos son congruentes si tienen dos ángulos congruentes y el lado común a ellos, también congruente.

 

Triángulos congruentes según el criterio LAL (lado-ángulo-lado)

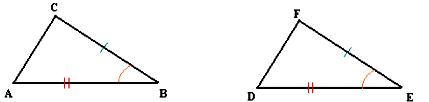
Se dice que el triángulo ABC es congruente con otro DEF si sus lados respectivos son congruentes y sus ángulos respectivos también los son.

Dos triángulos son congruentes si tienen dos lados congruentes y el ángulo comprendido por ellos también congruente.

 

Polígonos Congruentes

Un polígono es una figura geométrica plana limitada por al menos 3 segmentos rectos consecutivos no alineados, llamados lados. Por ejemplo, el hexágono es un polígono de seis lados.

La congruencia de polígonos puede estudiarse mediante la congruencia de triángulos.

Polígonos Congruentes:
Dos polígonos son congruentes si coinciden cuando colocamos uno sobre otro. Por ejemplo, dos triángulos son congruentes en cualquiera de los siguientes casos:
Tienen los 3 lados iguales (Criterio LLL)
Tienen 2 ángulos y un lado igual (Criterio ALA)
Tienen 2 lados iguales y e igual el ángulo comprendido(Criterio LAL),

dos cuadrados son congruentes si tienen el mismo lado, y así para el resto de los polígonos.

Figuras Congruentes:
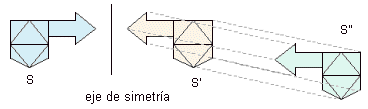
Se dice que dos figuras planas son congruentes si una de ellas puede ser convertida en la otra por medio de movimientos, tales como: rotación, traslación, simetría con respecto a una recta.
Ejemplo:
La figura que se muestra en la parte superior se observa que S es congruente con S', realizando los movimientos de simetría con respecto a una recta y una traslación de tal forma que éstas coincidan.

Para el resto de las figuras o polígonos, se dice que son congruentes cuando tienen tanto los segmentos como sus ángulos iguales.

Congruencia de Ángulos

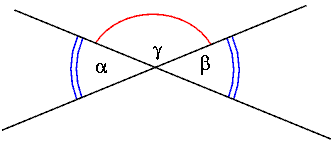
Dos ángulos son congruentes si tienen la misma medida en grados.
Por ejemplo, los siguientes ángulos son congruentes porque tienen la misma medida en grados.

Congruencia de Segmentos

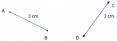
Dados dos puntos A y B, se le llama segmento AB a la intersección de la semirrecta de origen A que contiene al punto B, y la semirrecta de origen B que contiene al punto A. Luego, los puntos A y B se denominan extremos del segmento, y los puntos de la recta a la que pertenece el segmento (recta sostén), serán interiores o exteriores al segmento según pertenezcan o no a este.

Igualdad de segmentos 

La igualdad de segmentos, verificable por superposición, goza de las siguientes propiedades:

• Idéntica, reflexiva o refleja: Cualquier segmento es igual a sí mismo.
• Recíproca o simétrica: Si un segmento es congruente con otro, aquel es congruente con el primero.
• Transitiva: Si un segmento es congruente con otro, y este a su vez con un tercero, el primero es congruente con el tercero.

Consecuencia: Si dos igualdades entre segmentos tienen sus primeros miembros iguales, los segundos también lo son, y recíprocamente.

 

Noción de Congruencia

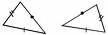
Noción de Congruencia

Dos figuras congruentes cuando al colocarlas una encima de otra de cierta manera, coinciden en todos sus puntos, segmentos y ángulos.

Congruencia

Se definen los conceptos siguientes:

• Segmento: Conjunto de puntos consecutivos limitados por otros dos puntos dentro de una recta.

• Ángulo: Un punto y un par de semirrectas que parten de él.

Sobre estos dos conceptos se postula la existencia de una relación de congruencia que es el equivalente axiomático de los movimientos. Básicamente, dados dos segmentos o dos ángulos, se acepta la existencia de un método que permite decir si son congruentes o no, basado en los siguientes postulados:

• Todo segmento es congruente consigo mismo.

• Si un segmento es congruente con uno dado, el dado es congruente con el primero.

• Si dos segmentos son congruentes con un tercero son congruentes entre ellos.

• Dados dos segmentos formando un ángulo, congruentes con otros dos que forman un ángulo congruente, al unir los extremos sueltos para formar dos triángulos, los tres lados y los tres ángulos serán congruentes.